马尔可夫链
马尔可夫链(Markov Chain, MC)是概率论和数理统计中具有马尔可夫性质(Markov property)且存在于离散的指数集(index set)和状态空间(state space)内的随机过程(stochastic process) [1-2] 。适用于连续指数集的马尔可夫链被称为马尔可夫过程(Markov process),但有时也被视为马尔可夫链的子集,即连续时间马尔可夫链(Continuous-Time MC, CTMC),与离散时间马尔可夫链(Discrete-Time MC, DTMC)相对应,因此马尔可夫链是一个较为宽泛的概念 [2] 。
马尔可夫链可通过转移矩阵和转移图定义,除马尔可夫性外,马尔可夫链可能具有不可约性、重现性、周期性和遍历性。一个不可约和正重现的马尔可夫链是严格平稳的马尔可夫链,拥有唯一的平稳分布。遍历马尔可夫链的极限分布收敛于其平稳分布 [1] 。
马尔可夫链被应用于蒙特卡罗方法中形成马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)方法 [2-3] ,也被用于动力系统、化学反应、排队论、市场行为和信息检索的数学建模。此外作为结构简单的马尔可夫模型(Markov model),诸多机器学习算法,包括隐马尔可夫模型(Hidden Markov Model, HMM)、马尔可夫随机场(Markov Random Field, MRF)和马尔可夫决策(Markov decision process, MDP)以马尔可夫链为理论基础 [4] 。
马尔可夫链的命名来自俄国数学家安德雷·马尔可夫(Андрей Андреевич Марков)以纪念其首次定义马尔可夫链和对其收敛性质所做的研究 [5] 。
中文名 马尔可夫链
外文名 Markov chain
类 型 随机过程
提出者 Andrey A. Markov
提出时间 1906年
学 科 统计学
应 用 数值模拟,机器学习
定义
马尔可夫链是一组具有马尔可夫性质的离散随机变量的集合。具体地,对概率空间 内以一维可数集为指数集(index set) 的随机变量集合 ,若随机变量的取值都在可数集内: ,且随机变量的条件概率满足如下关系 [2] :
则 被称为马尔可夫链,可数集 被称为状态空间(state space),马尔可夫链在状态空间内的取值称为状态 [2] 。这里定义的马尔可夫链是离散时间马尔可夫链(Discrete-Time MC, DTMC),其具有连续指数集的情形虽然被称为连续时间马尔可夫链(Continuous-Time MC, CTMC),但在本质上是马尔可夫过程(Markov process) [15] 。常见地,马尔可夫链的指数集被称为“步”或“时间步(time-step)” [2] 。
上式在定义马尔可夫链的同时定义了马尔可夫性质,该性质也被称为“无记忆性(memorylessness)”,即下一步的随机变量 在给定其当前步随机变量 后与其余的随机变量条件独立(conditionally independent): [2] 。在此基础上,马尔可夫链具有强马尔可夫性(strong Markov property),即对任意的停时( stopping time),马尔可夫链在停时前后的状态相互独立 [1] 。
n-阶马尔可夫链(n-order Markov chain)
n-阶马尔可夫链拥有n阶的记忆性,可视为马尔可夫链的推广。类比马尔可夫链的定义,n-阶马尔可夫链满足如下条件:
按上式,传统的马尔可夫链可以认为是1-阶马尔可夫链 [16] 。由马尔可夫性质可得,将多个马尔可夫链作为组元可以得到n-阶的马尔可夫链。
历史
马尔可夫链的提出来自俄国数学家安德雷·马尔可夫(Андрей Андреевич Марков)。马尔可夫在1906-1907年间发表的研究中为了证明随机变量间的独立性不是弱大数定律(weak law of large numbers)和中心极限定理(central limit theorem)成立的必要条件,构造了一个按条件概率相互依赖的随机过程,并证明其在一定条件下收敛于一组向量,该随机过程被后世称为马尔可夫链 [1] [5-6] 。
在马尔可夫链被提出之后,保罗·埃伦费斯特(Paul Ehrenfest)和Tatiana Afanasyeva在1907年使用马尔可夫链建立了Ehrenfest扩散模型(Ehrenfest model of diffusion) [7] 。1912年亨利·庞加莱(Jules Henri Poincaré)研究了有限群上的马尔可夫链并得到了庞加莱不等式(Poincaré inequality) [8-9] 。
1931年,安德雷·柯尔莫哥洛夫(Андрей Николаевич Колмогоров)在对扩散问题的研究中将马尔可夫链推广至连续指数集得到了连续时间马尔可夫链,并推出了其联合分布函数的计算公式 [10] 。独立于柯尔莫哥洛夫,1926年,Sydney Chapman在研究布朗运动时也得到了该计算公式,即后来的Chapman-Kolmogorov等式 [10] 。二十世纪50年代,前苏联数学家Eugene Borisovich Dynkin完善了柯尔莫哥洛夫的理论并通过Dynkin公式(Dynkin formula)将平稳马尔可夫过程与鞅过程(martingale process)相联系 [11-12] 。此后以马尔可夫链和马尔可夫过程为基础,各类马尔可夫模型被相继提出并在实际问题中得到应用了 [13] [14] 。
理论与性质
转移理论
马尔可夫链中随机变量的状态随时间步的变化被称为演变(evolution)或转移(transition)。这里介绍描述马尔可夫链结构的两种途径,即转移矩阵和转移图,并定义了马尔可夫链在转移过程中表现出的性质。
转移概率(transition probability)与转移矩阵(transition matrix)
主词条:转移矩阵
马尔可夫链中随机变量间的条件概率可定义为如下形式的(单步)转移概率和n-步转移概率 [2] :
式中下标 表示第n步的转移。由马尔可夫性质可知,在给定初始概率 后,转移概率的连续乘法可以表示马尔可夫链的有限维分布(finite-dimensional distribution) [2] :
式中的 为样本轨道(sample path),即马尔可夫链每步的取值 [2] 。对n-步转移概率,由Chapman–Kolmogorov等式可知,其值为所有样本轨道的总和 [2] :
上式表明,马尔可夫链直接演变n步等价于其先演变n-k步,再演变k步(k处于该马尔可夫链的状态空间内)。n-步转移概率与初始概率的乘积被称为该状态的绝对概率。
若一个马尔可夫链的状态空间是有限的,则可在单步演变中将所有状态的转移概率按矩阵排列,得到转移矩阵 [2] :
马尔可夫链的转移矩阵是右随机矩阵(right stochastic matrix),矩阵的第 行表示 时 取所有可能状态的概率(离散分布),因此马尔可夫链完全决定转移矩阵,转移矩阵也完全决定马尔可夫链 [17] 。由概率分布的性质可得,转移矩阵是一个正定矩阵,且每行元素之和等于1:
按相同的方式也可定义n-步转移矩阵: ,由n-步转移概率的性质(Chapman–Kolmogorov等式)可知,n-步转移矩阵是其之前所有转移矩阵的连续矩阵乘法: [2] 。
转移图(transition graph)
1. 可达(accessible)与连通(communicate)
马尔可夫链的演变可以按图(graph)结构,表示为转移图(transition graph),图中的每条边都被赋予一个转移概率。通过转移图可引入“可达”和“连通”的概念:
若对马尔可夫链中的状态 有: ,即采样路径上的所有转移概率不为0,则状态 是状态 的可达状态,在转移图中表示为有向连接: 。如果 互为可达状态,则二者是连通的,在转移图中形成闭合回路,记为 [1] 。由定义,可达与连通可以是间接的,即不必在单个时间步完成。
连通是一组等价关系,因此可以构建等价类(equivalence classes),在马尔可夫链中,包含尽可能多状态的等价类被称为连通类(communicating class) [1] 。
2. 闭合集(closed set)与吸收态(absorbing state)
给定状态空间的一个子集,若马尔可夫链进入该子集后无法离开: ,则该子集是闭合的,称为闭合集,一个闭合集外部的所有状态都不是其可达状态。若闭合集中只有一个状态,则该状态是吸收态,在转移图中是一个概率为1的自环。一个闭合集可以包括一个或多个连通类。
3. 转移图的例子
这里通过一个转移图的例子对上述概念进行举例说明 [1] :
转移图的例子
转移图的例子 [1]
由定义可知,该转移图包含了三个连通类: 、三个闭合集: 和一个吸收态,即状态6。注意到,在上述转移图中,马尔可夫链从任意状态出发终都会进入吸收态,这类马尔可夫链被称为吸收马尔可夫链(absorbing Markov chain) [18] 。
性质
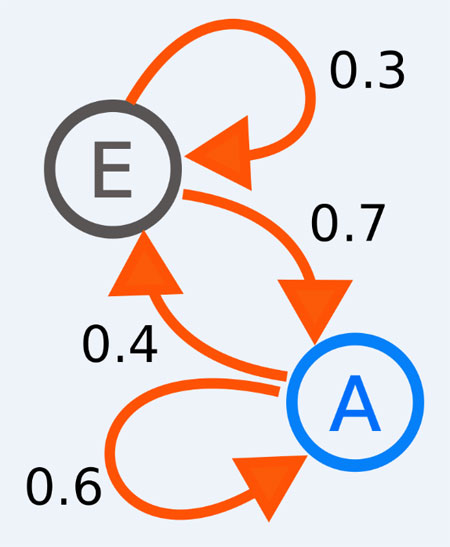
周期为3的不可约马尔可夫链
周期为3的不可约马尔可夫链
这里对马尔可夫链的4个性质:不可约性、重现性、周期性和遍历性进行定义。与马尔可夫性质不同,这些性质不是马尔可夫链必然拥有的性质,而是其在转移过程中对其状态表现出的性质。上述性质都是排他的,即不具有可约性的马尔可夫链必然是不可约的,以此类推。
不可约性(irreducibility)
如果一个马尔可夫链的状态空间仅有一个连通类,即状态空间的全体成员,则该马尔可夫链是不可约的,否则马尔可夫链具有可约性(reducibility) [19] 。马尔可夫链的不可约性意味着在其演变过程中,随机变量可以在任意状态间转移 [1] 。
重现性(recurrence)
若马尔可夫链在到达一个状态后,在演变中能反复回到该状态,则该状态具有重现性,或该马尔可夫链具有(局部)重现性,反之则具有瞬变性(transience)的。正式地,对状态空间中的某个状态,马尔可夫链对一给定状态的返回时间(return time)是其所有可能返回时间的下确界(infimum) [1] :
若 ,则该状态不存在瞬变性或重现性的;若 ,则该状态的瞬变性和重现性的判断准则如下 [1] :
在时间步趋于无穷时,可重现状态的返回概率(return probability)的和,即总访问次数的期望也趋于无穷:
此外,若状态 具有重现性,则可计算其平均重现时间(mean recurrence time) [1] :
若平均重现时间 ,该状态是“正重现的(positive recurrent)”,否则为“零重现的(null recurrent)” [1] 。若一个状态是零重现的,那意味着马尔可夫链两次访问该状态的时间间隔的期望是正无穷 [20] 。
由上述瞬变性和重现性的定义可有如下推论:
推论:对有限个状态的马尔可夫链,其至少有一个状态是可重现的,且所有可重现状态都是正可重现的 [20] 。
推论:若有限个状态的马尔可夫链是不可约的,则其所有状态是正重现的。
推论:若状态A是可重现的,且状态B是A的可达状态,则A与B是连通的,且B是可重现的 [21] 。
推论:若状态B是A的可达状态,且状态B是吸收态,则B是可重现状态,A是瞬变状态。
推论:由正可重现状态组成的集合是闭合集,但闭合集中的状态未必是可重现状态 [21] 。
周期性(periodicity)
一个正重现的马尔可夫链可能具有周期性,即在其演变中,马尔可夫链能够按大于1的周期重现其状态。正式地,给定具有正重现性的状态 ,其重现周期按如下方式计算 [1] :
式中 表示取集合元素的大公约数。举例说明,若在转移图中,一个马尔可夫链重现某状态需要的步数为 ,则其周期是3,即重现该状态所需的小步数。若按上式计算得到 ,该状态具有周期性,若 ,该状态具有非周期性(aperiodicity) [1] 。由周期性的定义可有如下推论:
推论:吸收态是非周期性状态。
推论:若状态A与状态B连通,则A与B周期相同 [1] 。
推论:若不可约的马尔可夫链有周期性状态A,则该马尔可夫链的所有状态为周期性状态 [1] 。
遍历性(ergodicity)
若马尔可夫链的一个状态是正重现的和非周期的,则该状态具有遍历性 [1] 。若一个马尔可夫链是不可还原的,且有某个状态是遍历的,则该马尔可夫链的所有状态都是遍历的,被称为遍历链。由上述定义,遍历性有如下推论:
推论:若状态A是吸收态,且A是状态B的可达状态,则A是遍历的,B不是遍历的。
推论:若多个状态的马尔可夫链包含吸收态,则该马尔可夫链不是遍历链。
推论:若多个状态的马尔可夫链形成有向无环图,或单个闭环,则该马尔可夫链不是遍历链。
遍历链是非周期的平稳马尔可夫链,有长时间尺度下的稳态行为,因此是被广泛研究和应用的马尔可夫链 [1] [2] 。
稳态分析
这里介绍马尔可夫链的长时间尺度行为的描述,即平稳分布和极限分布,并定义平稳马尔可夫链。
平稳分布(stationary distribution)
给定一个马尔可夫链,若在其状态空间存在概率分布 ,且该分布满足以下条件:
则 是该马尔可夫链的平稳分布。式中 是转移矩阵和转移概率,等价符号右侧的线性方程组被称为平衡方程(balance equation)。进一步地,若马尔可夫链的平稳分布存在,且其初始分布是平稳分布,则该马尔可夫链处于稳态(steady state) [1] 。从几何观点,考虑马尔可夫链的平稳分布有 ,因此该分布的支撑集是一个正单纯形(standard simplex)。
对不可约的马尔可夫链,当且仅当其存在唯一平稳分布,即平衡方程 在正单纯形上有唯一解时,该马尔可夫链是正重现的,且平稳分布有如下表示 [1] [19] :
上述结论被称为平稳分布准则(stationary distribution criterion) [1] 。对不可约和可重现的马尔可夫链,求解平衡方程可得到除尺度外唯一的特征向量,即不变测度(invariant measure),若该马尔可夫链是正重现的,则其平稳分布是求解平衡方程时得到的,特征值为1时的特征向量,即归一化后的不变测度 [2] ,因此马尔可夫链存在平稳分布的充要条件是其存在正重现状态。此外通过举例可知,若一个马尔可夫链包含多个由正重现状态组成的连通类(由性质可知它们都是闭合集,所以该马尔可夫链不是正重现的),则每个连通类都拥有一个平稳分布,且演变得到的稳态取决于初始分布。
极限分布(limiting distribution)
若一个马尔可夫链的状态空间存在概率分布 并满足如下关系:
则该分布是马尔可夫链的极限分布。注意到极限分布的定义与初始分布无关,即对任意的初始分布,当时间步趋于无穷时,随机变量的概率分布趋于极限分布 [2] 。按定义,极限分布一定是平稳分布,但反之不成立,例如周期性的马尔可夫链可能具有平稳分布,但周期性马尔可夫链不收敛于任何分布,其平稳分布不是极限分布 [22] 。
1. 极限定理(limiting theorem)
两个独立的非周期平稳马尔可夫链,即遍历链如果有相同的转移矩阵,那么当时间步趋于无穷时,两者极限分布间的差异趋于0。按随机过程中的耦合(coupling)理论,该结论的表述为:对状态空间相同的遍历链 ,给定任意初始分布后有 [2] :
式中 表示上确界(supremum)。考虑平稳分布的性质,该结论有推论:对遍历链 ,当时间步趋于无穷时,其极限分布趋于平稳分布 [2] :
该结论有时被称为马尔可夫链的极限定理(limit theorem of Markov chain),表明若马尔可夫链是遍历的,则其极限分布是平稳分布。对一个不可约和非周期的马尔可夫链,其是遍历链等价于其极限分布存在,也等价于其平稳分布存在 [2] [23] 。
2. 遍历定理(ergodic theorem)
若一个马尔可夫链为遍历链,则由遍历定理,其对某一状态的访问次数与时间步的比值,在时间步趋于无穷时趋近于平均重现时间的倒数,即该状态的平稳分布或极限分布 [1] :
遍历定理的证明依赖于强大数定律(Strong Law of Large Numbers, SLLN),表明遍历链无论初始分布如何,在经过足够长的演变后,对其中一个随机变量进行多次观测(极限定理)和对多个随机变量进行一次观测(上式左侧)都可以得到极限分布的近似 [1] 。由于遍历链满足极限定理和遍历定理,因此MCMC通过构建遍历链以确保其在迭代中收敛于平稳分布 [24] 。
平稳马尔可夫链(stationary Markov chain)
若一个马尔可夫链拥有唯一的平稳分布且极限分布收敛于平稳分布,则按定义等价于,该马尔可夫链是平稳马尔可夫链 [2] 。平稳马尔可夫链是严格平稳随机过程,其演变与时间顺序无关 [2] :
由极限定理可知,遍历链是平稳马尔可夫链。此外由上述定义,平稳马尔可夫链的转移矩阵是常数矩阵,n-步转移矩阵则是该常数矩阵的n次幂 [17] 。平稳马尔可夫链也被称为齐次马尔可夫链(time-homogeneous Markov chain)与之对应的,若马尔可夫链不满足上述条件,则被称为非平稳马尔可夫链(non-stationary Markvo chain)或非齐次马尔可夫链(time-inhomogeneous Markov chain) [25] 。
若平稳马尔可夫链对其任意两个状态满足细致平衡(detailed balance)条件,则其具有可逆性,被称为可逆马尔可夫链(reversible Markov chain) [26] :
马尔可夫链的可逆性是更严格的不可约性,即其不仅可以在任意状态间转移,且向各状态转移的概率是相等的,因此可逆马尔可夫链是平稳马尔可夫链的充分非必要条件。在马尔可夫链蒙特卡罗(Markvo chain Monte Carlo, MCMC) 中,构建满足细致平衡条件的可逆马尔可夫链,是确保其以采样分布为平稳分布的方法 [26] 。
特例
伯努利过程(Bernoulli process)
主词条:伯努利过程
伯努利过程也被称为二项马可夫链(Binomial Markov chain),其建立过程如下:给定一系列相互独立的“标识”,每个标识都是二项的,按概率 取正和负。令正随机过程 表示n个标识中有k个正标识的概率,则其是一个伯努利过程,其中的随机变量服从二项分布(binomialdistribution) [2] :
由建立过程可知,增加的新标识中正标识的概率与先前正标识的数量无关,具有马尔可夫性质,因此伯努利过程是一个马尔可夫链 [2] 。
赌徒破产问题(gambler's ruin)
参见:赌徒输光定理
假设赌徒持有有限个筹码在赌场下注,每次下注以概率 赢或输一个筹码,若赌徒不断下注,则其持有的筹码总数是一个马尔可夫链,且有如下转移矩阵 [2] :
赌徒输光筹码是吸收态,由一步分析(one-step analysis)可知,当 时,该马尔可夫链必然进入吸收态,即赌徒无论持有多少筹码,随着赌注的进行终都会输光。
随机游走(random walk)
主词条:随机游走
定义一系列独立同分布(independent identically distributed, iid)的整数随机变量 ,并定义如下随机过程 [2] :
则随机过程 是整数集内的随机游走,而 是步长。由于步长是iid的,因此当前步与先前步相互独立,该随机过程是马尔可夫链 [2] 。伯努利过程和赌徒破产问题都是随机游走的特例 [2] 。
由上述随机游走的例子可知,马尔可夫链有一般性的构建方法,具体地,若状态空间 内的随机过程 有满足形式 [2] :
其中, , 为空间 的iid随机变量且独立于 ,则随机过程 是马尔可夫链,其一步转移概率为: [2] 。该结论表明,马尔可夫链可以由 区间内服从iid均匀分布的随机变量(随机数)进行数值模拟 [2] 。
推广
马尔可夫过程(Markov process)
主词条:马尔可夫过程
马尔可夫过程也被称为连续时间马尔可夫链,是马尔可夫链或离散时间马尔可夫链的推广,其状态空间是可数集,但一维指数集不再有可数集的限制,可以表示连续时间。马尔可夫过程与马尔可夫链的性质是可以类比的,其马尔可夫性质通常有如下表示 [2] :
由于马尔可夫过程的状态空间是可数集,在连续时间下其样本轨道几乎必然(a.s.)是右连续的片段函数,因此马尔可夫过程可以表示为跳跃过程(jump process)并与马尔可夫链相联系 [2] :
式中 是某个状态的滞留时间(sojourn time), 是顺序的指数集成员(时间片段)。满足上述关系的马尔可夫链 和滞留时间 是跳跃过程 在有限个时间片段下的局部嵌入过程(locally embedded process) [2] 。
马尔可夫模型(Markov model)
主词条:马尔可夫模型
马尔可夫链或马尔可夫过程不是唯一以马尔可夫性质为基础建立的随机过程,事实上,隐马尔可夫模型、马尔可夫决策过程、马尔可夫随机场等随机过程/随机模型都具有马尔可夫性质并被统称为马尔可夫模型。这里对马尔可夫模型的其它成员做简要介绍:
1. 隐马尔可夫模型(Hidden Markov Model, HMM)
HMM是一个状态空间不完全可见,即包含隐藏状态(hidden status)的马尔可夫链,HMM中可见的部分被称为输出状态(emission state),与隐藏状态有关,但不足以形成完全的对应关系。以语音识别(speech recognition)为例,需要识别的语句是不可见的隐藏状态,接收的语音或音频是和语句有关的输出状态,此时HMM常见的应用是基于马尔可夫性质从语音输入推出其对应的语句,即从输出状态反解隐藏状态 [14] 。
2. 马尔可夫决策过程(Markov decision process, MDP):
MDP是在状态空间的基础上引入了“动作”的马尔可夫链,即马尔可夫链的转移概率不仅与当前状态有关,也与当前动作有关。MDP的一个例子是下棋,智能体对下一步棋的决策取决于当前的盘面和对手当前的动作,其中决策(policy)是状态到动作的映射。MDP是强化学习(reinforcement learning)方法的重要实现,被用于计算决策所得到的“回报”,即值函数(value function)。深度强化学习是使用深度学习(deep learning)方法求解值函数极大值所对应决策的优化过程 [27] 。MDP的推广之一是部分可观察马尔可夫决策过程(partially observable Markov decision process, POMDP),即考虑了HMM中隐藏状态和输出状态的MDP。
3. 马尔可夫随机场(Markov Random Field, MRF)
MRF是马尔可夫链由一维指数集向高维空间的推广。MRF的马尔可夫性质表现为其任意一个随机变量的状态仅由其所有邻接随机变量的状态决定。 类比马尔可夫链中的有限维分布,MRF中随机变量的联合概率分布是所有包含该随机变量的团(cliques)的乘积。MRF常见的例子是伊辛模型(Ising model) [13] [28] 。
哈里斯链(Harris chain)
哈里斯链是马尔可夫链从可数状态空间向连续状态空间的推广,给定可测空间 上的平稳马尔可夫链 ,若对可测空间的任意子集 和子集的返回时间 ,该马尔可夫链满足 [29] :
则该马尔可夫链是哈里斯可重现(Harris recurrent)的,被称为哈里斯链,式中的 是可测空间的σ-有限测度(σ-finite measure) [29] 。
应用
MCMC
构建以采样分布为极限分布的马尔可夫链是马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)的核心步骤,MCMC通过在马尔可夫链上运行大量的时间步得到近似服从采样分布的随机数,并使用这些随机数逼近求解目标对采样分布的数学期望 [2] [3] :
马尔可夫链的极限分布性质决定了MCMC是无偏估计(unbiased estimation),即采样数趋于无穷时会得到求解目标数学期望的真实值,这将MCMC与其替代方法,例如变分贝叶斯估计(variational Bayesian inference)相区分,后者计算量通常小于MCMC但无法得到无偏估计 [30] 。
其它
在物理学和化学中,马尔可夫链和马尔可夫过程被用于对动力系统进行建模,形成了马尔可夫动力学(Markov dynamics) [31-32] 。 在排队论(queueing theory)中,马尔可夫链是排队过程的基本模型 [33] 。在信号处理方面,马尔可夫链是一些序列数据压缩算法,例如Ziv-Lempel编码的数学模型 [34-35] ,在金融领域,马尔可夫链模型被用于预测企业产品的市场占有率 [36]







